泊松过程
定义
$\{N(t), t \geqslant 0\}$为泊松过程要满足下面四个条件:
- $N(0)=0$且为计数过程
- 独立增量过程:$\forall 0<t_{1}<t_{2}<\cdots<t_{n}$,有$N\left(t_{1}\right), N\left(t_{2}\right)-N\left(t_{1}\right), \cdots, N\left(t_{n}\right)-N\left(t_{n-1}\right)$相互独立
- 增量平稳性:$\forall s, t \geqslant 0, n \geqslant 0, P[N(s+t)-N(s)=n]=P[N(t)=n]$
- $\forall t>0$和充分小的$\Delta t>0$,有$\left\{\begin{array}{l}{P[N(t+\Delta t)-N(t)=1]=\lambda \Delta t+o(\Delta t)} \\ {P[N(t+\Delta t)-N(t) \geqslant 2]=o(\Delta t)}\end{array}\right.$
- 补充:$N(t)$表示在$[0,t]$内事件发生次数,有$P[N(s+t)-N(s)=k]=\frac{(\lambda t)^{k}}{k !} \mathrm{e}^{-\lambda t}, \quad k \in \mathbb{N}_{0}$
与随机过程符号的关系
- 令$S_0=0$,$S_n$表示第$n$个事件发生的时间
- $X_n=S_n-S_{n-1}$表示第$n-1$个事件和第$n$个事件发生的间隔
- 则两项等价$(N(t) \geqslant n)=\left(S_{n} \leqslant t\right)$,$(N(t)=n)=\left(S_{n} \leqslant t<S_{n+1}\right)=\left(S_{n} \leqslant t\right)-\left(S_{n+1} \leqslant t\right)$
定理:计数过程$\{N(t), t \geqslant 0\}$是泊松过程,当且仅当,$\{X_n,n \ge 1\}$独立服从$\lambda$的指数分布
- $X_k\sim \exp(\lambda)$,即$S_n=\sum_{i=1}^{n}X_i \sim\Gamma(n,\lambda)$
剩余寿命与年龄
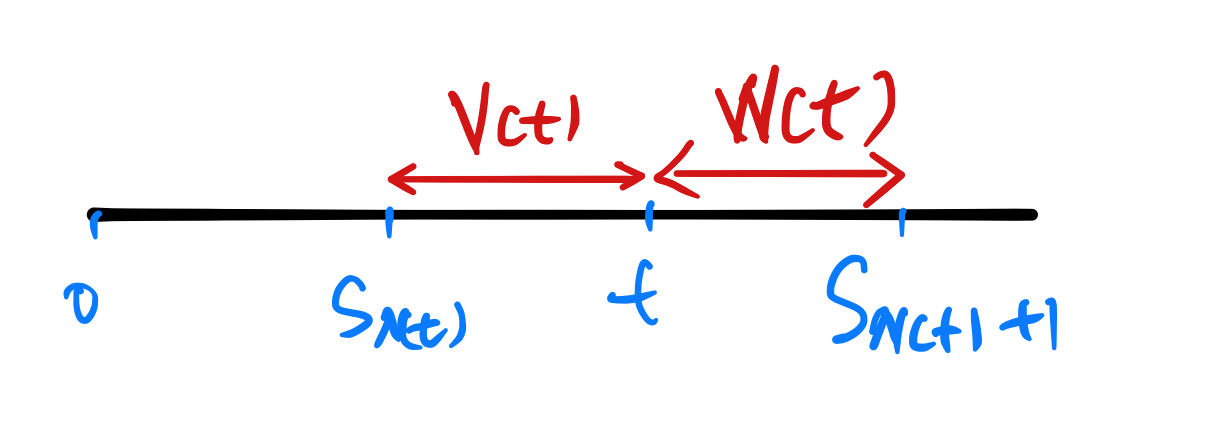
- $S_{N(t)}$表示在$t$时刻之前最后一个事件发生时间
- $S_{N(t)+1}$表示在$t$时刻之后第一个事件发生时间
- $V(t)$表示年龄
- $W(t)$表示剩余寿命,在$t$时刻观察,剩余的寿命
性质:
$P(W(t) \leqslant x)=1-\exp (-\lambda x), \quad x \geqslant 0$
$P(V(t) \leqslant x)=\left\{\begin{array}{ll}{1-\exp (-\lambda x),} & {0 \leqslant x<t} \\ {1,} & {t \leqslant x}\end{array}\right.$
- $P(W(t)>x)=1-F(x+t)+\int_{0}^{t} P(W(t-u)>x) \mathrm{d} F(u)$,其中$F(x)$是$X_n$的分布函数
到达时间
- 本节研究在$N(t)=n$的条件下,$S_1,\cdots,S_n$的条件分布
定理:$S_1,\cdots,S_n$相继发生时间(记为$t_i$)的条件概率密度为
$f\left(t_{1}, t_{2}, \cdots, t_{n}\right)=\left\{\begin{array}{ll}{\frac{n !}{t^{n}},} & {0<t_{1}<t_{2}<\ldots<t_{n} \leqslant t} \\ {0,} & others \end{array}\right.$
- 定理说明:在$N(t)=n$的条件下,$S_1,\cdots,S_n$的条件分布与$n$个$iid$的均匀分布顺序统计量的分布一样
非时齐泊松过程
这里放宽了平稳性的要求,即不要求$\lambda$是常数
定义:计数过程$\{N(t), t \geqslant 0\}$有强度$\{\lambda(t)>0, t \geqslant 0\}$
- $N(0)=0$
- $\{N(t), t \geqslant 0\}$为独立增量
- $P(N(t+h)-N(t)=1)=\lambda(t) h+o(h), \quad P(N(t+h)-N(t) \geqslant 2)=o(h)$
- 令$m(t)=\int_{0}^{t} \lambda(s) \mathrm{d} s$
- $\forall s, t \geqslant 0$有$P(N(s+t)-N(s)=n)=\frac{[m(s+t)-m(s)]^{n}}{n !} \exp \{-[m(s+t)-m(s)]\} \quad(n \geqslant 0)$
- 即有$N(t+s)-N(t)\sim Possion(m(t+s)-m(t))$
复合泊松过程
定义:$X(t)=\sum_{i=1}^{N(t)} Y_{i}$
其中$\{N(t), t \geqslant 0\}$是泊松过程,$Y_i$是$iid$的随机变量,且$N(t)$与$Y_i$独立
有$E[X(t)]=\lambda t E(Y)$,$Var[X(t)]=\lambda t E(Y^2)$