• 随机森林是基于决策树的分类方法
  • 随机森林的思路是一步一步提升的：决策树 $\rightarrow $ bagging $\rightarrow$ 随机森林

决策树

什么是决策树

  • 有$n$份样本$(Y_i,X_{i1},\cdots,X_{ip})$，这里$i= 1,\dots, n$，样本有$p$个特征

  • 对于某一份样本，通过$X_1 \cdots X_p$的各种抉择，最终得到结果$\hat{Y}=f(X)$

  • 下图为网络上找到一张示意图，$X=${女票，陪女票，任务，吃鸡}

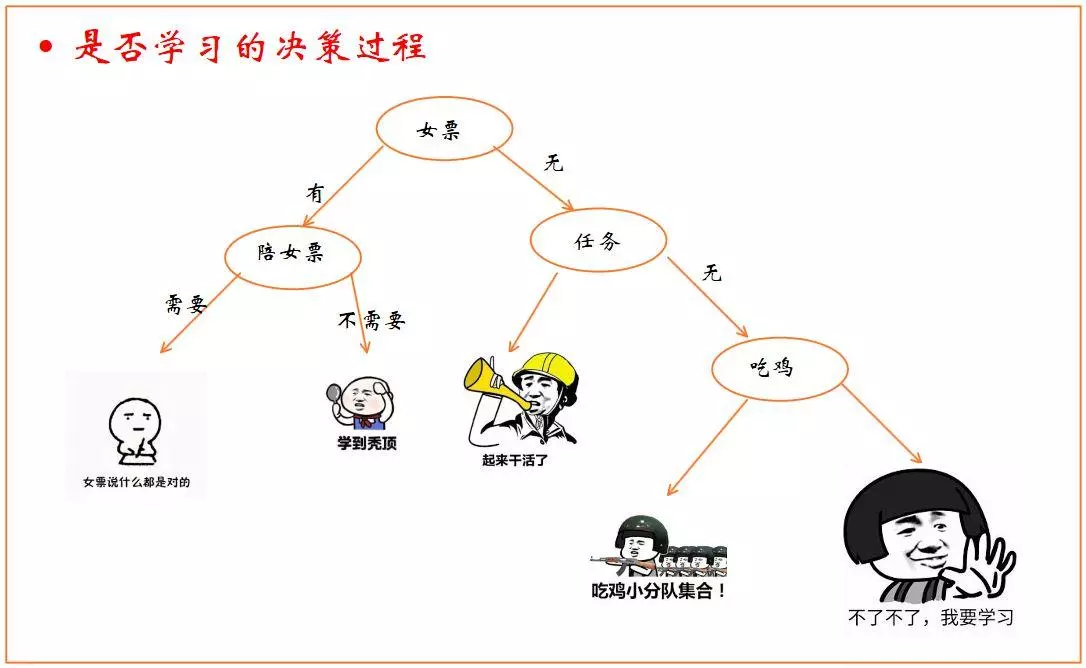
image-20191030104122466

  • 另一个简单的图，以两个$X = {X_1,X_2}$为例

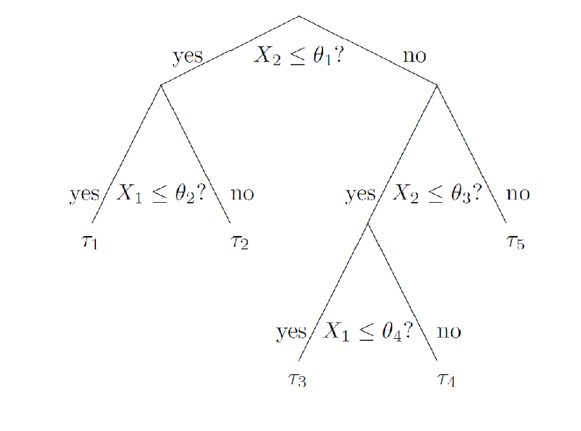
image-20191030104122466

​ 这里可以理解为，树将样本的特征空间（$X$的空间）划分成了几个不同的部分，每个部分对应一个结果

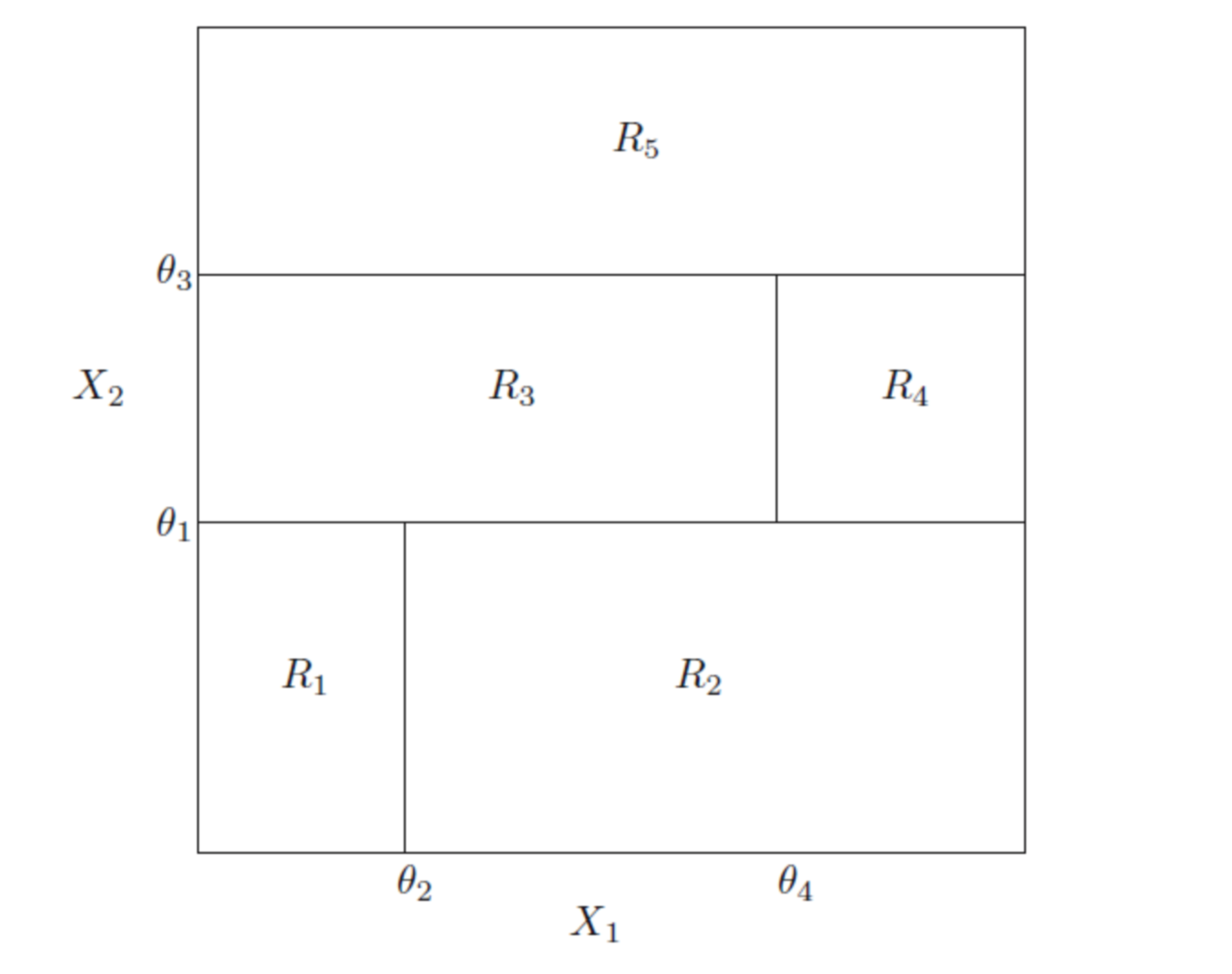
image-20191030104122466

如何生成树

  • 结点的分裂方式（$n$份样本）：
    • $X$是连续型、有序的离散型：每个结点有$n-1$种可能的分裂方法
    • $X$是无序的离散型：每个结点有$2^{n-1}-1$种可能的分裂方法
  • 不同的分裂方法，选择某个分裂方法的标准：
    • $Y$是连续性（就是回归模型）：均方误差
    • $Y$是离散型（分类模型）：不纯度

  • 不纯度的概念：

    • $Y$有$K$个类别，即最终的结果有$K$种，如上面的图就有五种类别，记为$\Pi_{1}, \dots, \Pi_{k}$

    • 不纯度函数$i(\tau)=\phi(p(1 | \tau), \ldots, p(K | \tau))$

    • $p(i | \tau)$是$P\left(X \in \Pi_{i} | \tau\right)$的点估计，即$p(k | \tau) = \sum_{i}^{n}I{(X_i\in \Pi_{k})}/n$

    • 常用的不纯度函数：

      • 错分率：$i(\tau)=1-\max _{k}(p(k | \tau))$
      • 熵函数：$i(\tau)=-\sum_{k=1}^{K} p(k | \tau) \log p(k | \tau)$
      • Gini指数：$i(\tau)=\sum_{k^{\prime}=1}^{K}\sum_{k \neq k^{\prime}}p(k | \tau) p\left(k^{\prime} | \tau\right)=1-\sum_{k}\{p(k | \tau)\}^{2}$

  • 对于一个节点$\tau$，计算一次不纯度

    • 沿不纯度下降最大的一个选择
    • 不纯度下降幅度小于阈值就继续分裂

  • 最后的叶子节点中，类别数最多的就是某个类

  • 补充：Gini与cart？？？？

举一个例子

样本 变量$X_1$ 变量$X_2$ $Y$
a 0.2 0.3 0
b -0.1 -1 0
c 0.2 -0.2 0
d 0 -0.3 1
e 0.2 2.6 1

  • 这里$K=2,n=5,p=2$

  • Gini不纯度函数为：$ i(\tau) = p(1|\tau)p(0|\tau)+p(0|\tau)p(1|\tau)=2p(0|\tau) \left(1-p(0|\tau) \right) $

  • 初始结点的Gini不纯度为：$ i_0 = 2\times0.6\times0.4=0.48 $

第一次分裂 左边结点不纯度 左边概率 右边结点不纯度 右边概率 不纯度减小值
$X_1 \le -0.1$ 0 0.2（b） 0.5 0.8(a,c,d,e) 0.48-0*0.2-0.5*0.8=0.08
$\cdots$
$X_2 \le 0.3$ 3/8 0.8(a,b,c,d) 0 0.2(e) 0.18
  • 上表中右边结点不纯度的0.5计算方式为：右边叶子结点有acde四个点，ac为0类，de为1类，概率分别为$2/4\ and\ 2/4$，则$ i(\tau) = 2 \times (2/4)\times(2/4) =0.5 $

修建树

  • R代码：
1
2
3
4
5
library(rpart)
fit = rpart(y~., data = , method = 'class') #分类树
fit = rpart(y~., data = , method = 'anova') #回归树
library(rpart.plot)
prp(fit) # 展示节点各类的数量

信息熵

  • 这里补充一点熵的概念
  • 什么是信息熵？
    • 确定性过程在数学里是司空见惯的现象，如$f(x)=x^2$这个函数，输入$x$，输出值是确定的。但是现实中大部分事物都存在不确定性（随机性），那么怎么去衡量这个不确定性呢？
    • “熵”就是关于不确定性的一个极好的数学描述
    • 1865年，Rudolf Julius Emanuel Clausius第一次使用了熵（entropy）的概念，用在热力学中

  • 信息熵：香农提出的，关于不确定的度量。这里的度量和我们平常使用的“公斤”、“千米”一样，是某种数值的度量单位。香农的信息熵本质上是对我们司空见惯的“不确定现象”的数学化度量

  • 假设我们有$n$个事件，每个事件的发生概率为$p_i (i=1,\dots,n)$，我们定义香农熵函数为$H$

    • 那么样本空间$(p_1, \dots, p_n)$中的一个点$(p_{1}^{}, \dots, p_{n}^{})$，该点的香浓熵为$H(p_{1}^{}, \dots, p_{n}^{})$
    • $H$函数有以下性质：
    • $\forall (p_{1}^{}, \dots, p_{n}^{}) $，有$H(p_{1}^{}, \dots, p_{n}^{}) \leq H(\frac{1}{n}, \dots, \frac{1}{n})$
    • $H(p_{1}^{}, \dots, p_{n}^{}) \leq H(\frac{1}{n}, \dots, \frac{1}{n})$是$n$的严格递增函数
    • 如果一个不确定事件分解成几个持续事件，则原先事件的不确定度等于持续事件不确定度的加权和
    • 对固定的自然数n，不确定度函数 H 是 (p1, p2, …, pn) 的一个连续函数