本文使用的教材为《Applied Linear Statistical Models》Fifth Edition，P1~P508
课本从简单的一元线性回归讲起，再引入矩阵，拓展到多元线性回归分析

一、线性回归的基本概念

1. 真实的模型与线性回归

我们有$n$个样本$(X_{i1},\cdots ,X_{i,p-1},Y_i)$，每个样本有真实的关系为$Y=f_{true}(X)+\varepsilon_{true}$
我们用线性关系拟合$f_{true}$，即响应变量$Y_i$和预测变量$X_i$满足关系$Y_{i}=\beta_{0}+\beta_{1} X_{i 1}+\beta_{2} X_{i 2}+\cdots+\beta_{p-1} X_{i, p-1}+\varepsilon_{i}, \quad i=1,2, \ldots, n$
矩阵形式为：$Y=X \beta+\varepsilon$，$Y \varepsilon$都是$n \times 1$的随机向量

$\boldsymbol{Y}=\left[\begin{array}{c}{Y_{1}} \\ {Y_{2}} \\ {\vdots} \\ {Y_{n}}\end{array}\right], \boldsymbol{X}=\left[\begin{array}{cccc}{1} & {X_{11}} & {\dots} & {X_{1, p-1}} \\ {1} & {X_{21}} & {\dots} & {X_{2, p-1}} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ {1} & {X_{n 1}} & {\dots} & {X_{n, p-1}}\end{array}\right], \boldsymbol{\beta}=\left[\begin{array}{c}{\beta_{0}} \\ {\beta_{1}} \\ {\vdots} \\ {\beta_{p-1}}\end{array}\right], \boldsymbol{\varepsilon}=\left[\begin{array}{c}{\varepsilon_{1}} \\ {\varepsilon_{2}} \\ {\vdots} \\ {\varepsilon_{n}}\end{array}\right]$

注意一点，在多个变量的线性回归中，变量之间不一定是相互独立的
矩阵形式有：$\varepsilon \sim N(\mathbf{0}_{n},\sigma^{2} \boldsymbol{I}_{n})$

# 例子
n = 1000
set.seed(1)
x1 = rnorm(n)
x2 = rnorm(n)
x3 = rnorm(n)
x4 = ifelse(rnorm(n) < 0, '0', '1')
y = 1*x1 + 2*x2 + 3*x3 + rnorm(n)
dat = as.data.frame(cbind(x1, x2, x3, x4, y))
# 拟合模型
fit = lm(y~., data = dat)

2. 线性回归的要求

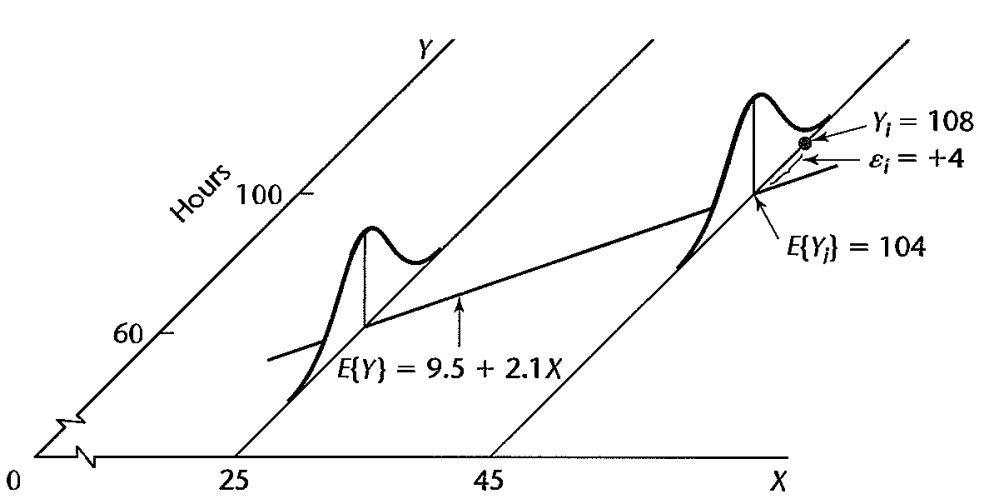
$Y$的趋势在不同$X$下是不同的，即在不同的$X$下，$Y$有不同的概率分布
$Y$的均值在不同的$X$下不同
$\beta_0 \beta_1$为参数，$X_i$看作已知的常数
$\varepsilon_i$看作随机变量，$E\left\{\varepsilon_{i}\right\}=0\quad \sigma^{2}\left\{\varepsilon_{i}\right\}=\sigma^{2}$
$\varepsilon_i$与$\varepsilon_j$不相关

3. 如何拟合参数

最小二乘法求参，矩阵形式为：
$\\ Q=(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{\beta})^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \boldsymbol{\beta})=\boldsymbol{Y}^{\prime} \boldsymbol{Y}-2 \boldsymbol{\beta}^{\prime} \boldsymbol{X}^{\prime} \boldsymbol{Y}+\boldsymbol{\beta}^{\prime} \boldsymbol{X}^{\prime} \boldsymbol{X} \boldsymbol{\beta}$ $\boldsymbol{b}=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \boldsymbol{Y}$
拟合后得到预测值$\hat{Y}=Xb=HY=X(X^TX)^{-1}X^TY$
残差$e_i = Y_i-\hat{Y_i}$，衡量预测值与观测值的差距
$\sigma^2$的估计值$s^{2}=MSE=\frac{\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}{p-1}$，有$E\{M S E\}=\sigma^{2}$

$Var(\hat{Y}) = \sigma^2H,\hat{Var}(\hat{Y})=MSE \cdot H$

> summary(fit)

Call:
lm(formula = y ~ ., data = dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-3.08689 -0.67290  0.01275  0.66285  2.98838 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.01375    0.04482   0.307    0.759    
x1           1.00473    0.03068  32.746   <2e-16 ***
x2           1.95967    0.03048  64.285   <2e-16 ***
x3           2.97810    0.03088  96.451   <2e-16 ***
x4          -0.03659    0.06360  -0.575    0.565    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.002 on 995 degrees of freedom
Multiple R-squared:  0.9387,	Adjusted R-squared:  0.9384 
F-statistic:  3808 on 4 and 995 DF,  p-value: < 2.2e-16

4. 正态线性模型

假定误差项$\varepsilon_i$独立服从$N(0,\sigma^2)$
这个模型很常用，所以经常要检验误差是否真的是正态

二、线性模型的统计推断

1. 检验整个模型

$H_{0}: \beta_{1}=\cdots=\beta_{p-1}=0,\quad H_{a}: \beta_{k} \neq 0$ for at least one $k$
构造统计量$F=\frac{M S R}{M S E}$，有$F \sim F(p-1, n-p)$
就是summary(fit)的最后一行

1	F-statistic: 3808 on 4 and 995 DF, p-value: < 2.2e-16

2. 检验某个系数

$H_{0}: \beta_{k}=0,\quad H_{a}: \beta_{k} \neq 0$
构造统计量$t_{k}=\frac{b_{k}-\beta_{k}}{s\left\{b_{k}\right\}} \sim t(n-p)$
就是summary(fit)中每个变量后的t检验，如x4的p值0.565，有理由认为x4的系数为0

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.01375    0.04482   0.307    0.759    
x1           1.00473    0.03068  32.746   <2e-16 ***
x2           1.95967    0.03048  64.285   <2e-16 ***
x3           2.97810    0.03088  96.451   <2e-16 ***
x4          -0.03659    0.06360  -0.575    0.565

3. 多个系数的检验

还可以构造多个系数的统统检验
$H_{0}: \beta_{k_{i}}=0, i=1,2, \ldots, g, \quad H_{a}: \beta_{k_{i}} \neq 0,$ for some $i=1,2, \dots, g$，这里的$g< p-1$
构造统计量$F=\frac{\operatorname{SSE}(R)-\operatorname{SSE}(F) /\left(d f_{R}-d f_{F}\right)}{\operatorname{SSE}(F) / d f_{F}}=\frac{\operatorname{SSE}(R)-\operatorname{SSE}(F) / g}{\operatorname{SSE}(F) /(n-p)}$
其实这个就是General Linear Test Approach的思想

4. $E(Y_h)$的区间估计

上述提到在不同的$X$下，$Y$有不同的概率分布，也即给定了$X_h$，$Y_h$有一个概率分布，现在来估计$Y_h$的均值的置信区间
我们感兴趣的是$E(Y_h)$，但是只有$\hat{Y_h}$，所以通过$\hat{Y_h}$来估计$E(Y_h)$
有$ E\left\{\hat{Y}_{h}\right\} =E\left\{Y_{h}\right\} \quad \sigma^{2}\left\{\hat{Y}_{h}\right\} =\sigma^{2}\left[\frac{1}{n}+\frac{\left(X_{h}-\bar{X}\right)^{2}}{\sum\left(X_{i}-\bar{X}\right)^{2}}\right]$
$\frac{\hat{Y}_{h}-E\left\{Y_{h}\right\}}{s\left\{\hat{Y}_{h}\right\}}$服从$t(n-2)$，即$1-\alpha$的置信区间为$\hat{Y}_{h} \pm t(1-\alpha / 2 ; n-2) s\left\{\hat{Y}_{h}\right\}$

1
2
3

new_x = data.frame(x = seq(-3, 3, 0.5)) # 新的点
# E(Y_h)的区间估计
pred = predict(fit, newdata = new_x, interval = 'confidence')# 注意这里是confidence

5. 新的预测$Y_{h(new)}$

假设我们已经拟合了一个模型$\widehat{Y}_{h}=b_{0}+b_{1} X_{h}$，现在给一个新的值$X_{h(new)}$，我们感兴趣的是预测真实值而不是均值
即有$Y_{h(n e w)}=\beta_{0}+\beta_{1} X_{h}+\epsilon_{h(n e w)}$
当模型的$\beta$未知，有$\frac{Y_{h(n e w)}-\hat{Y}_{h}}{S\{\operatorname{Pred}\}} \sim t(n-2) \quad S\{\text {Pred}\}=\sqrt{M S E} \sqrt{1+\frac{1}{n}+\frac{\left(X_{h}-\bar{X}\right)^{2}}{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}}$
注意，这里和上面的$E(Y_h)$的区间估计不一样，统计量的分母不一样

1	pred = predict(fit, newdata = new_x, interval = 'prediction')

6. 方差分析

方差分析用于两个及两个以上样本均数差别的显著性检验。
其实方差分析就是线性回归
方差分解：$\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}=\sum_{i=1}^{n}\left(\hat{Y}_{i}-\bar{Y}\right)^{2}+\sum_{i=1}^{n}\left(Y_{i}-\hat{Y}_{i}\right)^{2}$，即$\mathrm{SSTO}=\mathrm{SSR}+\mathrm{SSE}$
方差分析表如下
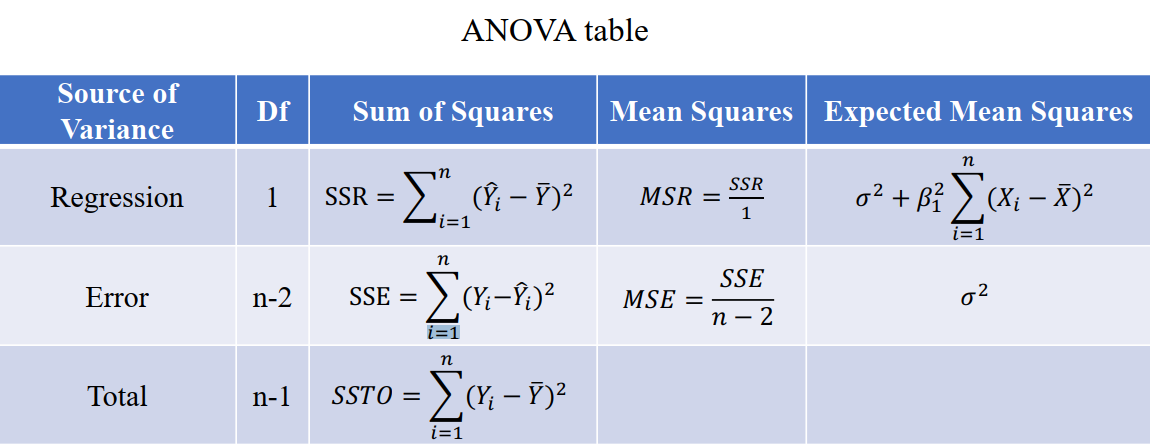
ANOVA F Test：$H_{0}: \beta_{1}=0\quad H_1: \beta_{1} \neq 0$，统计量$F^{*}=\frac{M S R}{M S E}\sim F(1, n-2)$

7. 拟合程度

$R$方：$\boldsymbol{R}^{2}=\frac{\boldsymbol{S S R}}{\boldsymbol{S S T O}}$，用于衡量模型的拟合程度
注意，R方并不一定越高越好，可能会出现误导。
Adjusted R方：$R_{a}^{2}=1-\frac{S S E /(n-p)}{S S T O /(n-1)}=1-\left(\frac{n-p}{p-1}\right) \frac{S S E}{S S T O}$

1	summary(fit)

8. Correlation分析

假设$X$和$Y$都是正态随机变量，令$\rho$为两个随机变量的相关系数
$E[Y | X]=\mu_{Y}+\rho \frac{\sigma_{Y}}{\sigma_{X}}\left(\mathrm{X}-\mu_{X}\right)$，即$\beta_{1}=\rho \frac{\sigma_{Y}}{\sigma_{X}}$，$\beta_0 = $
$\rho$的估计量$\mathrm{r}=\pm \sqrt{\frac{S S R}{S S T O}}=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}$
做统计推断$H_{0}: \rho=0 \quad$ vs $\quad H_{a}: \rho \neq 0$
统计量$T=\frac{r \sqrt{n-2}}{\sqrt{1-r}} \sim \mathrm{t}(\mathrm{n}-2)$，这个跟$F$检验是一样的

三、线性模型的诊断与补救措施

1. 残差

什么是残差：在$Y_{i}=\beta X_i+\varepsilon_{i}$的模型下，$e_i = Y_i-\hat{Y_i}$
- $\mathrm{E}\left(e_{i}\right)=0$，$\operatorname{Var}\left(e_{i}\right)=\left[1-\frac{1}{n}-\frac{\left(X_{i}-\bar{X}\right)^{2}}{\sum_{\mathrm{t}=1}^{n}\left(X_{t}-\bar{X}\right)^{2}}\right] \sigma^{2}$，$\operatorname{Cov}\left(e_{i}, e_{j}\right)=-\left[\frac{1}{n}+\frac{\left(X_{i}-\bar{X}\right)\left(X_{j}-\bar{X}\right)}{\sum_{\mathrm{t}=1}^{n}\left(X_{t}-\bar{X}\right)^{2}}\right] \sigma^{2}$
- 当n很大且$X$分布比较好时，有$\operatorname{Var}\left(e_{i}\right) \cong \sigma^{2}, \operatorname{Cov}\left(e_{i}, e_{j}\right) \cong 0$
- 通常残差$e_i$在某种程度上可以当作随机误差$\varepsilon_{i}$

1	fit$residuals

学生化残差studentized residual：$e_{i}^{S}=\frac{e_{i}}{s\left\{e_{i}\right\}}$，$S\left\{e_{i}\right\}=\sqrt{M S E} \sqrt{1-\frac{1}{n}-\frac{X_{i}-\bar{X}}{\sum_{\mathrm{t}=1}^{n}\left(X_{t}-\bar{X}\right)^{2}}}$
- 这个名字的来源：计算$e_i^S$的过程很像统计推断，$e_i$除$s\{e_i\}$像统计量，像服从student t distribution，但是并不是真正的服从t分布
我们可以从残差图中看出一下几点：
- 回归方程是否线性
- 误差项的方差是否相同
- 误差项是否相互独立
- 误差项是否正态分布
- outlier
- 重要的预测变量$X$是否被忽略

# 检查同方差性
library(car)
> ncvTest(fit) # 这里p值为0.34343，不拒绝‘异方差性’的假设，虽然这很扯淡
Non-constant Variance Score Test 
Variance formula: ~ fitted.values 
Chisquare = 0.8975677, Df = 1, p = 0.34343
# 第二种检查异方差性的方法，看残差图

Test for Randomness：Durbin-Watson test
Test for constancy of error variance：Brown-Forsthe Test、Breusch-Pagan Test

2. 共线性

就是变量之间有严重的相关性，那么变量稍微变化，整个模型的预测值就会波动非常大。解决方法就是去掉一部分变量

3. 补救措施

当模型拟合不好时，主要有两个方面的措施：换模型（下面）、数据变换

四、回归模型的建模

我们有$p-1$个变量，那么就有$2^{p-1}$个模型（变量是否在模型中），当$p$很大时我们很难跑完所有的模型，那么需要一些评判标准来衡量模型的好坏
一般的评判标准：$\frac{SSE_p}{n}+\lambda(p)$，后者为惩罚项

常用的有Adjusted $R^{2}, C_{p}, M S E, P R E S S, A I C$ and $B I C$
- $R_{a, p}^{2}=1-\frac{n-1}{n-p} \frac{S S E(p)}{S S T O}=1-\frac{M S E(p)}{S S T O /(n-1)}$
- $C_{p}=\frac{S S E(p)}{M S E\left(X_{1}, X_{2}, \ldots, X_{P-1}\right)}-(n-2 p)$
- $AIC = n\log (\operatorname{SSE}(p))-n \log (n)+2 p$
- $BIC=\operatorname{n} \log (S S E(p))-n \log (n)+\log(n)p$
- $\operatorname{PRESS}(p)=\sum_{i=1}^{n}\left(Y_{i}-\hat{Y}_{i(i)}\right)^{2}$，其中$\hat{Y}_{i(i)}$是删去第$i$个样本拟合后，再对第$i$个样本做的预测
- $Y_{i}-\hat{Y}_{i(i)}=\frac{e_{i}}{1-h_{i i}}=\frac{Y_{i}-\hat{Y}_{i}}{1-h_{i i}}$，$h_{ii}$是$H$的第$i$个对角元素
选变量的方法：
- 子集选择（subset selection）
  - 最佳子集算法：选择一个评判标准，选择一些变量，如bess
  - 向前、向后逐步回归，如stepAIC
- 压缩估计（shrinkage）
  
  有最小二乘估计$\hat{\beta}_{(o l s)}=\underset{\beta}{\operatorname{argmin}}(Y-X \beta)^{T}(Y-X \beta)$
  
  加入惩罚项有$\phi(\beta)=(Y-X \beta)^{T}(Y-X \beta)+\lambda \boldsymbol{p}(\boldsymbol{\beta})$
  - 岭回归Ridge Regression：$p(\beta)=|| \beta||_{2}^{2}$
  - LASSO：$p(\beta)=|\beta|_{1}$
- 投影（projection related）