本文大部分内容来自油管教程和厚杰泰的《结构方程模型及其应用》

一、基本概念

《结构方程模型及其应用》里叙述：结构方程模型是验证性因子模型和潜变量（latent variable）因果模型（叫结构方程会不会更好一点？）的结合：

种类	作用
测量方程 measurement equation	描述潜变量（因子）与指标（可测量的变量）的关系
结构方程 structural equation	描述潜变量（因子）之间的关系

潜变量的概念：与可观察变量相对，是不可直接观察但是通过观察到的其他变量推断（通过数学模型）的变量（直接测量），有的地方叫因子
油管教程里提出的几个容易混淆的概念：
回归模型：$y = \beta_1 x_1 + \beta_2 x_2 + \epsilon$
路径模型：$z = \beta_1 x + \epsilon_1, \quad y = \beta_2 z + \epsilon_2$
- 注意这里路径模型和回归模型是不一样的，$x$预测$z$，$z$预测$y$，形成了一条链chain，这就有结构的意味了
因子模型： $\begin{align}y_1 &= F + e_1 \\ y_2 &= F + e_2 \\ y_3 &= F + e_3\end{align}$
- 变量之间相互影响，但是这种相互影响的结构是没办法直接观察到，通常会考虑correlation
- 所以会使用一个共同的影响因素$F$，来模拟这种相互关系
油管教程叙述：结构方程模型，综合了上面三种模型。在侯的书里，所有的公式都是线性回归的方式展示出来的，所以他没有提到回归模型。

例子1

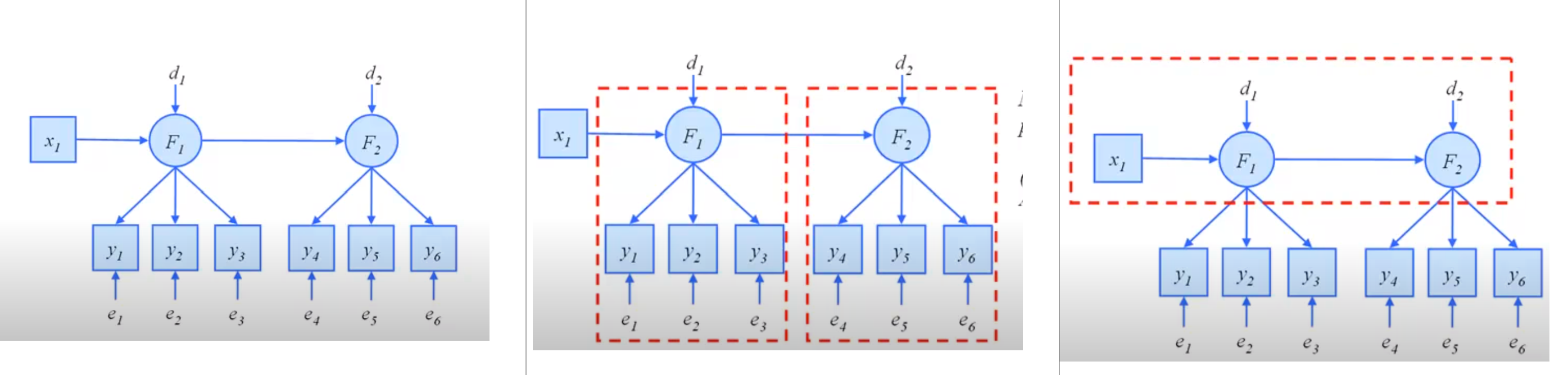
下面图来自油管的教程
左图就是我们设想的模型；中间图的红框，就是测量模型（因子分析）；右图的红框，就是结构模型，或者叫路径模型

二、模型假设

测量模型：$\mathrm{x} = \Lambda_\mathrm{x} \times \xi + \delta$，$\mathrm{y} = \Lambda_\mathrm{y}\ \eta + \epsilon$
结构模型：$\eta = B \times \eta + \Gamma \times \xi +\zeta$

符号解释：
- $x$为外源指标，y是内生指标，都是可以测量得到的变量。外源只起自变量作用。虽然分不分没啥区别。。
- $\Lambda$为系数矩阵（参数矩阵），也叫因子负荷矩阵
- $\delta$、$\epsilon$和$\zeta$为误差项
假设$\boldsymbol{E}(\epsilon) = 0$，$\boldsymbol{E}(\delta) = 0$，$\boldsymbol{cov}(\xi_i, \delta_j) = 0$，$\boldsymbol{cov}(\delta_i, \delta_j) = 0$
- 注意，$\boldsymbol{cov}(\delta_i, \delta_j) = 0$的假设不一定是必须的

$\boldsymbol{E}(\zeta) = 0$

例子2

下面为CFA的例子。这里我没有区别$x$和$y$，统一使用了$x$：

$\begin{array}{l}{x_{1}=\lambda_{11} \xi_{1}+\delta_{1}\\x_{2}=\lambda_{21} \xi_{1}+\delta_{2}\\x_{3}=\lambda_{31} \xi_{1}+\delta_{3}}\\{x_{4}=\lambda_{42} \xi_{2}+\delta_{4}\\x_{5}=\lambda_{52} \xi_{2}+\delta_{5}}\end{array}$

其中假定

$\begin{array}{l}\operatorname{E}(\delta_i) = 0\\\operatorname{cov}\left(\xi_{i}, \delta_{j}\right)=0\\\operatorname{cov}\left(\delta_{i}, \delta_{j}\right)=0\end{array}$

参数为$\lambda_{11}, \lambda_{21}, \lambda_{31}, \lambda_{42}, \lambda_{52}, \boldsymbol{\phi}_{11}=\operatorname{var}\left(\xi_{1}\right),\ \boldsymbol{\phi}_{22}=\operatorname{var}\left(\xi_{2}\right), \boldsymbol{\phi}_{21}=\operatorname{cov}\left(\xi_{2}, \boldsymbol{\xi}_{1}\right),\ \theta_{i i}=\operatorname{var}\left(\delta_{i}\right)$
矩阵形式为$x=\Lambda_{x} \xi+\delta$

$\boldsymbol{x}=\left(\begin{array}{l}{x_{1}} \\ {x_{2}} \\ {x_{3}} \\ {x_{4}} \\ {x_{5}}\end{array}\right), \boldsymbol{\Lambda}_{x}=\left(\begin{array}{ll}{\lambda_{11}} & {0} \\ {\lambda_{21}} & {0} \\ {\lambda_{31}} & {0} \\ {0} & {\lambda_{42}} \\ {0} & {\lambda_{52}}\end{array}\right), \boldsymbol{\xi}=\left(\begin{array}{l}{\xi_{1}} \\ {\xi_{2}}\end{array}\right), \boldsymbol{\delta}=\left(\begin{array}{c}{\delta_{1}} \\ {\delta_{2}} \\ {\delta_{3}} \\ {\delta_{4}} \\ {\delta_{5}}\end{array}\right)$

我们写出$\operatorname{var}(\mathrm{X})$的协方差矩阵，从上述模型推导出的协方差矩阵。只写下三角部分

$\mathbf{\Sigma}=\left[\begin{array}{llll}{\operatorname{var}\left(x_{1}\right)} & {} & {} & {} \\ {\operatorname{cov}\left(x_{2}, x_{1}\right)} & {\operatorname{var}\left(x_{2}\right)} & {} \\ {\operatorname{cov}\left(x_{3}, x_{1}\right)} & {\operatorname{cov}\left(x_{3}, x_{2}\right)} & {\operatorname{var}\left(x_{3}\right)} \\ {\operatorname{cov}\left(x_{4}, x_{1}\right)} & {\operatorname{cov}\left(x_{4}, x_{2}\right)} & {\operatorname{cov}\left(x_{4}, x_{3}\right)} & {\operatorname{var}\left(x_{4}\right)} \\ {\operatorname{cov}\left(x_{5}, x_{1}\right)} & {\operatorname{cov}\left(x_{5}, x_{2}\right)} & {\operatorname{cov}\left(x_{5}, x_{3}\right)} & {\operatorname{cov}\left(x_{5}, x_{4}\right)} & \operatorname{var}\left(x_{5}\right)\end{array}\right]$ $\boldsymbol{\Sigma}(\boldsymbol{\theta})=\left[\begin{array}{llll}{\lambda_{11}^{2}\phi_{11}+\theta_{11}} & {} & {} & {} \\ {\lambda_{21} \lambda_{11} \phi_{11}} & {\lambda_{21}^{2} \phi_{11}+\theta_{22}} & {} \\ {\lambda_{31} \lambda_{11} \phi_{11}} & {\lambda_{31} \lambda_{21} \phi_{11}} & {\lambda_{31}^{2} \phi_{11}+\theta_{33}} \\{\lambda_{42} \lambda_{11} \phi_{21}} & {\lambda_{42} \lambda_{21} \phi_{21}} & {\lambda_{42} \lambda_{31} \phi_{21}} & {\lambda_{42}^{2} \phi_{22}+\theta_{44}} \\{\lambda_{52} \lambda_{11} \phi_{21}} & {\lambda_{52} \lambda_{21} \phi_{21}} & {\lambda_{52} \lambda_{31} \phi_{21}} & {\lambda_{52} \lambda_{42} \phi_{22}} & {\lambda_{52}^{2} \phi_{22}+\theta_{55}}\end{array}\right]$

当有样本时，用样本的协方差矩阵代替$\mathbf{\Sigma}$，与$\boldsymbol{\Sigma}(\boldsymbol{\theta})$的元素一一对应，就可以解出参数。

# R代码
library(lavvan)
model = 'eplison_1 =~ x_1 + x_2 + x_3
eplison_2 =~ x_3 + x_4'
fit = cfa(model, data)

例子3

这里举一个路径模型的例子，为了方便，写成矩阵的形式

$\mathrm{y} = B \mathrm{y} + \Gamma \mathrm{x} + \zeta$

假设：$\mathrm{E}(\zeta) = \mathrm{0},\quad \mathrm{cov}(x, \zeta) = \mathrm{0}$
总体的真实的协方差矩阵为$\Sigma$，根据上面模型推出来的协方差矩阵为$\Sigma(\theta)$
做变换：$y=(I-B)^{-1}(\Gamma x+\zeta)=\tilde{B}(\Gamma x+\zeta)$，令$\tilde{\boldsymbol{B}}=(\boldsymbol{I}-\boldsymbol{B})^{-1}$、$\boldsymbol{\Sigma}_{x x}(\boldsymbol{\theta}) = \boldsymbol{\Phi}$，则有

$\begin{aligned} \boldsymbol{\Sigma}(\boldsymbol{\theta}) &=\left(\begin{array}{cc} \boldsymbol{\Sigma}_{y y}(\boldsymbol{\theta}) & \boldsymbol{\Sigma}_{y x}(\boldsymbol{\theta}) \\ \boldsymbol{\Sigma}_{x y}(\boldsymbol{\theta}) & \boldsymbol{\Sigma}_{x x}(\boldsymbol{\theta}) \end{array}\right) \\ &=\left(\begin{array}{cccc} \tilde{\boldsymbol{B}}\left(\boldsymbol{\Gamma} \boldsymbol{\Phi} \boldsymbol{\Gamma}^{\prime}+\boldsymbol{\Psi}\right) \tilde{\boldsymbol{B}}^{\prime} & \tilde{\boldsymbol{B}} \boldsymbol{\Gamma} \boldsymbol{\Phi} \\ \boldsymbol{\Phi} \boldsymbol{\Gamma}^{\prime} \boldsymbol{\tilde { B }}^{\prime} & \boldsymbol{\Phi} \end{array}\right) \end{aligned}$

如果这个模型是真的，那么有$\boldsymbol{\Sigma}=\boldsymbol{\Sigma}(\boldsymbol{\theta})$，前者用样本协方差矩阵来估计，就可以求得参数了。

三、R包

整个SEM都是使用lavvan包的，附带R包的pdf：lavvan包使用说明
知乎lavvan用法

1
2
3

=~： 用来定义潜变量，用在cfa模型上
~ ： 用来定义回归关系方程，用在路径分析上
~~： 用来定义协方差，用于限定一些参数

例子4

model <- '
   # latent variables
     ind60 =~ x1 + x2 + x3
     dem60 =~ y1 + y2 + y3 + y4
     dem65 =~ y5 + y6 + y7 + y8
   # regressions
     dem60 ~ ind60
     dem65 ~ ind60 + dem60
   # residual covariances
     y1 ~~ y5
     y2 ~~ y4 + y6
     y3 ~~ y7
     y4 ~~ y8
     y6 ~~ y8
'
fit <- sem(model,data=PoliticalDemocracy)
summary(fit)
# 查看拟合效果
fitMeasures(fit)
# 画图
library(semPlot)
semPaths(fit)