Efficient Estimation of Word Representations in Vector Space
Distributed Representations of Words and Phrases and their Compositionality
第一篇文章在NNLM的基础上做了修改，提出了CBOW和skip-gram模型
第二篇文章暂时还没看，大概是讲skip-gram的
这里感谢知乎的回答，大部分博客都只讲原理，不讲输入输出流，其实这对模型的理解不够
知乎cbow 与 skip-gram的比较讲得比较好
参考github博客和知乎，CSDN

介绍

首先提出了以往的NLP，大多将words视为原子级别的单位，不可再分；没有词之间的相关性这种概念。选择这种模型的好处是，简单、稳定、简单模型在大量数据训练的效果好优于复杂模型在小数据集上的效果。很有名的模型就是n-gram
本文的目的是，学习高质量的word vectors，也就是词向量、NNLM中的feature vector
在这篇文章之前，没有人可以在hundred of miilions of words，这个数量级上，使用50~100维的word vectors
本文希望，相似的词语应该彼此相邻，而且词语之间有多维度的相似，have multiple degrees of similarity
文中提到了屈折语Inflectional Language，百度给的定义是：屈折语的一个词缀经常同时表达多种意思，而黏着语的一个词缀一般倾向于只表达单一种的意思

模型结构

模型的计算复杂度为$O=E \times T \times Q$。$E$是训练的epochs，$T$是训练集中的词语个数（注意不是$V$），$Q$是模型结构
NNLM的模型复杂度为，$N$是前面的词的个数，$D$是词向量的维度，$H$是隐藏层的维度

$Q=N \times D+N \times D \times H+H \times V$

虽然可以用层次softmax来提高计算速度，但是，上面模型最大的瓶颈在于隐藏层，计算量为$N \times D \times H$
文章的第三节，提出了两种方法来训练语言模型
具体的模型如下图

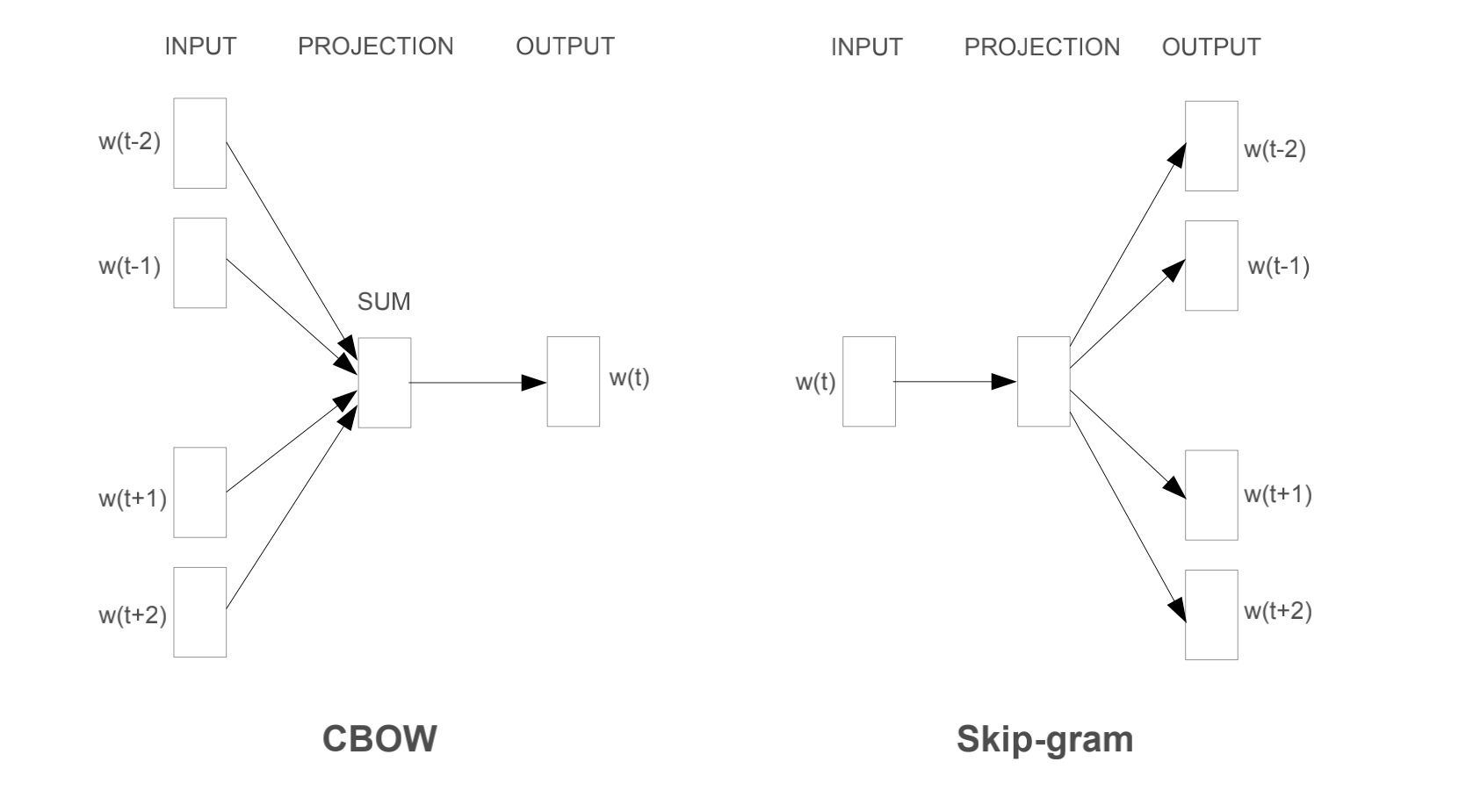
Continuous Bag-of-Words Model

这就是鼎鼎大名的CBOW
这个模型在NNLM的基础上，去掉了非线性的隐藏层，投影层是所有词语共享的，不是投影矩阵
这个模型叫做词袋模型，是因为序列中的词语顺序不影响投影
模型复杂度是

$Q=N \times D+D \times \log _{2}(V)$

Continuous Skip-gram Model

这是本文提出的第二个模型，这个和CBOW很相似，但是这个是反着来的
这里是用当前的词语，放到log-linear的分类器中，预测当前词前后一定范围内的词
文中发现，增大范围可以提高词向量的质量。因为更远的词，通常比近距离的词的相关性更弱，也就是更偏向于独立，所以它的权重应该更小
模型复杂度如下，$C$是词语的最大距离，每次训练的时候，从$1\sim C$中随机抽一个范围$R$，也就是要预测$2R$个单词
模型复杂度

$Q=C \times\left(D+D \times \log _{2}(V)\right)$

注意：skip-gram的模型，输入是词语对
- 如，我今天很高兴
- 中间词是很，左右窗宽为2，那么模型的输入是[很，今]，[很，天]，[很，高]，[很，兴]

细节

如何评价词向量的质量，文中定义了一个综合测试集，包含五种类型的语义问题，九种句法问题。每种问题通过两个步骤产生：相似的词语对由手工建立；将两个词语对相连接形成问题。
比如，文中手工建立了城市这几个词语，然后问这些城市属于哪个州
注意，在文中，词语的输入输出是one-hot形式，再经过词向量矩阵才会取出相应的词向量，但是在代码中，直接使用inputs来取词向量矩阵中的数字
正常的CBOW的计算流程应该是：
- 输入一个词语序列，如我、天，形成两个one-hot向量
- one-hot向量经过词向量矩阵，取出两个词向量，如$E_{\text{我}}$和$E_{\text{天}}$
- 将两个词向量相加平均，对应下面的torch.sum
- 注意：输入输出的embbeding，不是同一个，有时候我把$W^{‘}$看做是$W$的转置，一直没整明白
- 具体的模型如下，注意两个矩阵叫做embedding matrix和context matrix，是不一样的

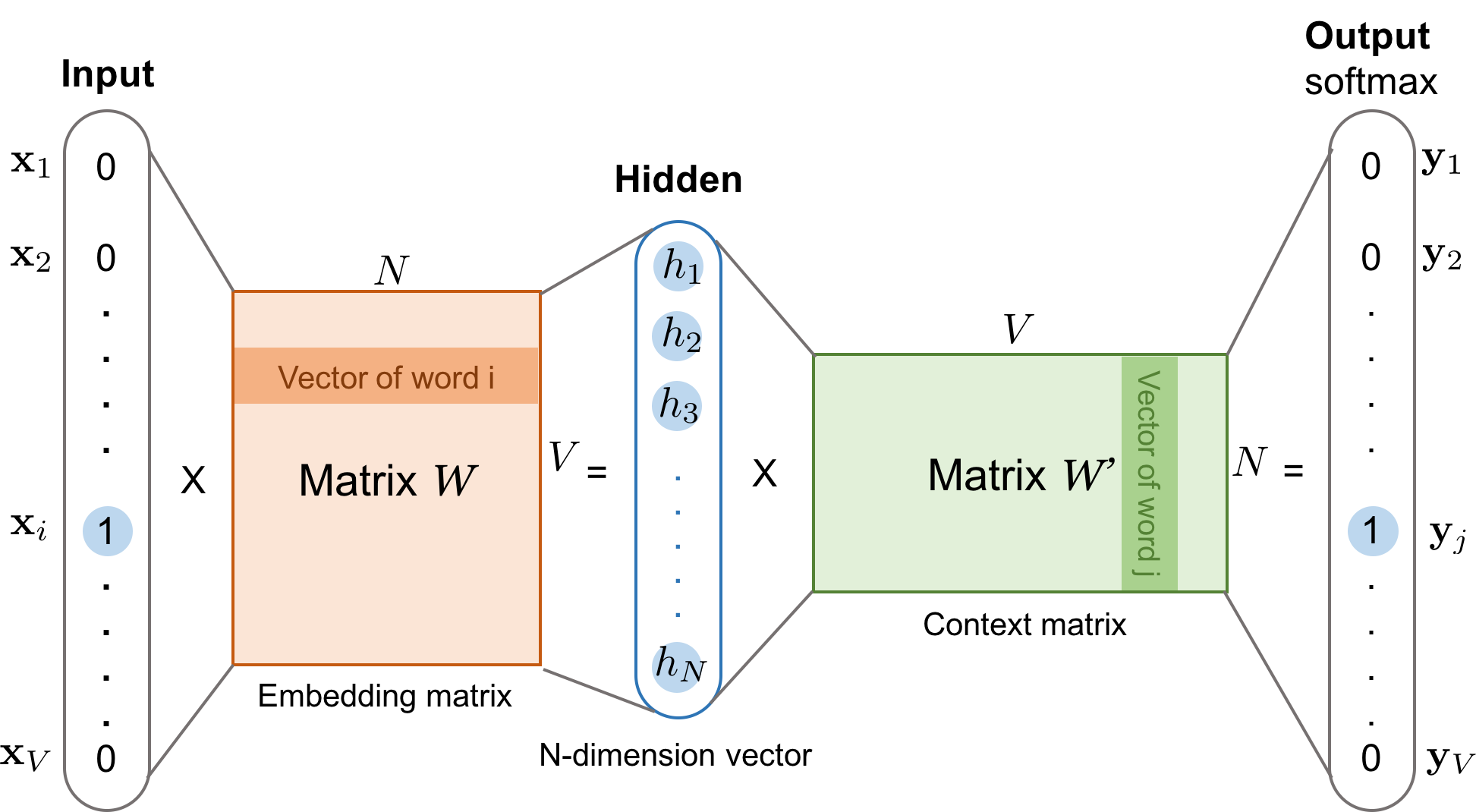
skip gram的计算类似上面的方式

完整的loss

在上面的计算过程中，最终的output是$|V|$维的向量，也就是给出了预测的词语的概率
也就是下面的公式，$v_{\text{input}}$是输入的词语的词向量，$v_{w_{O}}^{\prime}$是上面context matrix中的某一列，也就代表了预测的某个词语的内容向量
CBOW和skip gram不同之处，也可以从loss函数中看得出来
- CBOW的$v_{\text{input}}$是，多个词向量的平均值（或者sum），所以给定一个样本，只有一个loss
- skip gram的$v_{\text{input}}$是，单个词向量；所以一个样本，会有窗口大小，这么多个loss

$p\left(w_{O} \mid \text{input} \right)=\frac{\exp \left(v_{w_{O}}^{\prime}{ }^{\top} v_{\text{input}}\right)}{\sum_{i=1}^{V} \exp \left(v_{w_{i}}^{\prime}{ }^{\top} v_{\text{input}}\right)}$

第二篇文章

现在记录下第二篇文章
文中说道，对词频进行下采样（这里是对词频高的词语进行下采样吗？），提高了训练速度，提高了词频较少的词语的准确率
这里提到了Noise Contrastive Estimation
词向量表示的方法，有局限性，比如很难表示惯用词，比如Boston Globe是新闻报纸，但是两个词不是自然合并在一起的；所以现在用的是单词，不是短语；那么从单词过渡到短语，可以这么做，先准备大量的短语的语料，再将短语视为单独的token
skip-gram模型就是在最大化，平均log probability
- 下面的$t$是指，长度为$T$的词语序列中，第$t$个单词，$c$是窗宽
- $c$越大，训练样本越多，会导致更高的准确率

$\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p\left(w_{t+j} \mid w_{t}\right)$

层次softmax

这里的问题是想解决，最后计算概率的时候，更快一点
原来的softmax，慢的问题在于，要对所有的单词的context vector，计算向量内积，再归一化得到概率。如果我们的单词有几十万个，那么就要计算几十万次，这就很浪费了
所以现在不想用softmax，改用哈夫曼树的结构，作者把这个叫做层次softmax
哈夫曼树，每个节点都是一个单词
- 哈夫曼树的构建：每次合并数值（这里是词频）最小的两个节点
- 构建完之后，每个单词都可以用唯一的0和1的编码来表示
层次softmax
用原论文的符号表示
$n(w, j)$是从根节点到第$j$个节点的路径，$L(w)$是路径长度
- 由于文中的llbracketlatex符号打不出来，所以用$g$来表示；g(true)=1, g(false)=-1
- $\sigma$是sigmoid函数

$p\left(w \mid w_{I}\right)=\prod_{j=1}^{L(w)-1} \sigma\left\{ g \left[ n(w, j+1)=\operatorname{ch}(n(w, j)) \right] \cdot v_{n(w, j)}^{\prime}{ }^{\top} v_{w_{I}}\right\}$

上面的概率写得并不好，很晦涩，用下面的写法，就明白了
- 在哈夫曼树上，从根节点走到对应的结点（也就是上文中的预测的词语），每到一个结点，都是一次二选一，即选择向左走、向右走，那么就是一个二分类问题，所以用了一个简单的逻辑回归的形式
- 没看懂文章中的$ch$是啥意思
- 当$n(w, j+1)=\operatorname{ch}(n(w, j))$时，就是路径中，走对了方向；换句话说，假设$ch$永远是这个结点的左孩子，那么路径中的下一个结点就是左孩子
- 当$n(w, j+1)!=\operatorname{ch}(n(w, j))$时，即路径中的下一个结点就是右孩子
- 这就变成了一个判断左右的二分类问题；

$p(w \mid \operatorname{Context}(w))=\prod_{j=2}^{L{(w)}} p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)$

负采样

Noise Contrastive Estimation是噪声对比估计，即一个好的模型，应该可以区分数据与噪声
这里注意，在上面给定输入输出的时候，其实就已经知道输入的$w$对应的词向量，和输出的词$w_{target}$，那会得到一个logit，即$\exp\{ w * w_{target}^T \}$
负采样的就是，在词典中抽取其他的词语当做负样本，抽样的方法是带权重的抽样
- 权重是$\frac{w}{\sum w}$，词频归一化作为权重，文中提到了$3/4$的缩放
- $\operatorname{len}(w)=\frac{[\operatorname{counter}(w)]^{\frac{3}{4}}}{\sum_{u \in \mathcal{D}}[\operatorname{counter}(u)]^{\frac{3}{4}}} .$
负采样之后，就是计算：

$\log \sigma\left(v_{w_{O}}^{\prime}{ }^{\top} v_{w_{I}}\right)+\sum_{i=1}^{k} \mathbb{E}_{w_{i} \sim P_{n}(w)}\left[\log \sigma\left(-v_{w_{i}}^{\prime}{ }^{\top} v_{w_{I}}\right)\right]$

代码

CBOW的代码实现

class cbow(torch.nn.Module):
    def __init__(self, nwords, emb_size):
        super(cbow, self).__init__()
        #input matrix
        self.emb = torch.nn.Embedding(nwords, emb_size)
        #output matrix
        self.projection = torch.nn.Linear(emb_size, nwords)

    def forward(self, words):
        emb = self.emb(words)
        emb_sum = torch.sum(emb, dim=0) # emb_size
        emb_sum = emb_sum.view(1, -1) # 1, emb_size
        out = self.projection(emb_sum)
        
        log_probs = F.log_softmax(out, dim = 1)
        return log_probs

skipgram的代码实现

class skip(torch.nn.Module):
    def __init__(self, nwords, emb_size):
        super(skip, self).__init__()
        #input matrix
        self.embeddings_input = torch.nn.Embedding(nwords, emb_size)
        #output matrix
        self.embeddings_context = torch.nn.Parameter(torch.randn(emb_size, nwords))

    def forward(self, input_word, context_word):
 				emb_input = self.embeddings_input(input_word) # bs, emb_dim
        emb_context = self.embeddings_context(context_word)  # bs, emb_dim

        emb_product = torch.mul(emb_input, emb_context)     # bs, emb_dim
        emb_product = torch.sum(emb_product, dim=1)          # bs
        loss = -F.logsigmoid(emb_product)      
        
        return loss