没想到这篇文章时代如此久远，是Rumelhart David E、Hinton Geoffrey E、Williams Ronald J 三位大神在1985年发表的
年代久远，以至于没有数字版本的pdf。。。
阅读这篇文章，了解最开始的RNN的想法
这篇文章不知道有几个版本，我找到的每篇都不太一样。。
- http://www.cs.utoronto.ca/，这份pdf只有四页，这篇文章的题目是Learning representations by back-propagating errors
- stanford的版本，足足23页；这篇文章的题目是learning internal representations by error propagation
- 这两个不一样，本文主要讲第一个文章
首先文章描述了一种新的学习过程，反向传播；这种学习过程是神经元的学习过程
这个过程，就是重复的调整权重，来最小化网络输出值和真实值之间的差距
由于权重的不过调整，所以中间的隐藏单元就可以来表示重要的特征
文章在第一段就提到，如果不加隐藏神经元，那么，输入和输出是直接相连的，所以上面提到的调整权重，是很简单的；但是加了隐藏的神经单元，调整权重就变得困难了；整个学习过程，必须决定哪个神经元必须激活、来帮助缩小后面的真实值和输出值
最简单的网络应该是这样的：输入有一层，中间有许多层，输出有一层，连接的方式必须是从下面的层往上传递，不能从上面的层往下传，同时，可以跳过中间层
- 这里想到了ResNet，也是使用了skip connection的方式，解决了残差问题
- 为什么只能从下面的层往上传递，不能从上面的层往下传递？
每一层的方式都是这样，其中$j$是指：这一层的输入，第$j$个位置，是上一层output（即$y_i$）的线性和

$x_{j}=\sum_{i} y_{i} w_{i j}$

接着，这个神经元，也就是$x_j$的值，要经过非线性激活函数，这里是sigmoid
- 为什么要激活？

$y_{j}=\frac{1}{1+e^{-x_{j}}}$

文中定义的，损失函数如下，$c$是样本下标，$j$是输出值的下表

$E=\frac{1}{2} \sum_{c} \sum_{j}\left(y_{j c}-d_{j c}\right)^{2}$

最小化$E$，也就是，使用梯度下降的方法；那么就需要计算$E$的偏导数；上面提到的学习过程，包括前向传播，和反向传播
反向传播就是，将梯度从最顶层传递到最底层

文中的例子

文章举了一个特殊的例子，如下图，这是一个族谱图，可以转成三元组的形式：<人名><关系><人名>

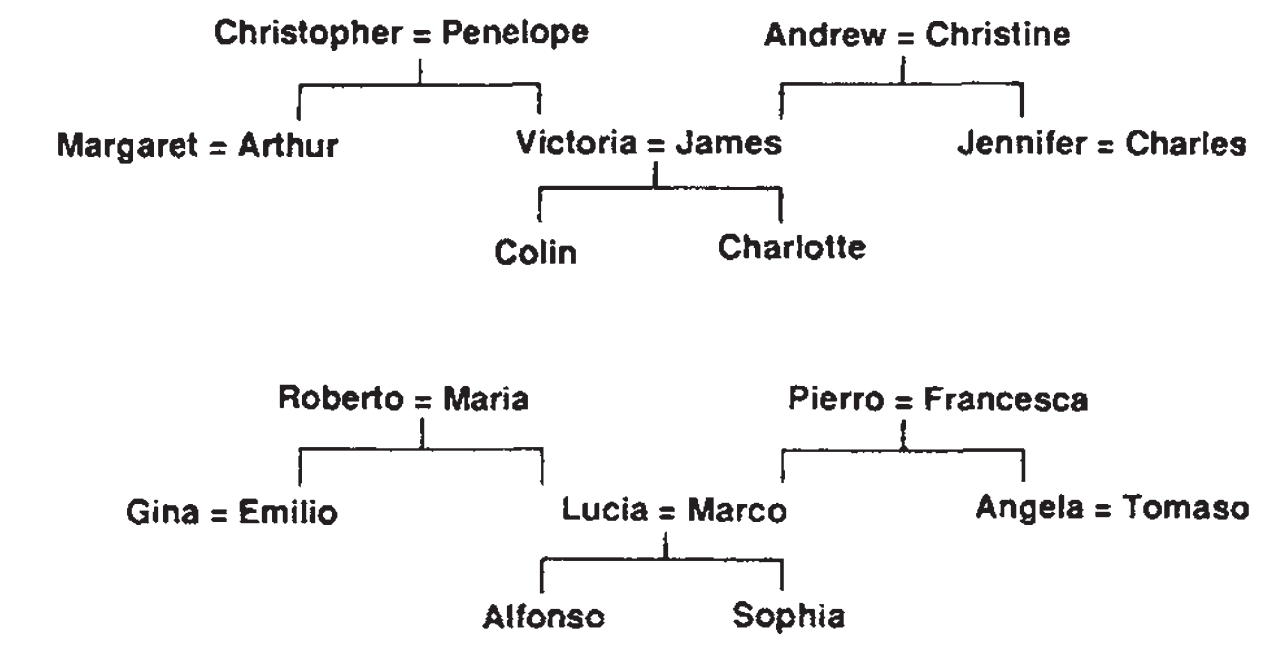
现在的网络是要，给定三元组的前两个，预测第三个，即预测人名

反向传播算法

首先对$E$计算偏导数，如下，这里的计算，是对某个$c$来说的，也就是计算这个样本的梯度

$\frac{ \partial E}{ \partial y_{j} } =y_{j}-d_{j}$

根据链式法则，那么可以计算出，激活函数之前，权重的偏导数

$\frac{\partial E} {\partial x_{j}} = \frac{\partial E} { \partial y_{j}} \cdot \frac{\mathrm{dy}_{\mathrm{j}}}{ \mathrm{d} x_{j} }$

注意，上面的第二项，是对激活函数求导，所以没有偏导数，而激活函数式sigmoid，所以可以写成下面的形式

$\frac{\partial E} {\partial x_{j}} = \frac{\partial E} { \partial y_{j}} \cdot y_j \left(1-y_j\right)$

注意，这里可以看得出来，$x_j$是怎么影响误差的：有了$x_j$之后，可以计算出$y_j$，而$\frac{\partial E} { \partial y_{j}}$在上面的表达形式中，有$\frac{\partial E} { \partial y_{j}}=y_j - d_j$
- 那么就有$\frac{\partial E} {\partial x_{j}} = (y_j - d_j) \cdot y_j \cdot (1-y_j)$
而$x_j$是下面一层神经网络的输出的线性和，即$x_{j}=\sum_{i} y_{i}^{(t-1)} w_{i j}$，为了区分两个层的$y$，底层的$y$的上标加了$t-1$
也就是，我们可以计算出，这些权重是怎么影响最终的误差的

$\frac{\partial E} {\partial w_{ij}} = \frac{\partial E} { \partial x_{j}} \cdot \frac{\partial {x_j}}{ \partial w_{ij}} = (y_j - d_j) \cdot y_j \cdot (1-y_j) * y_{i}^{(t-1)}$

上面说的是，最后一层的偏导计算方式
有了偏导数之后，就可以更新权重了

$\Delta w=-\varepsilon \partial E / \partial w$

文章中还提到了另外一种方式，即当前的梯度更新值，结合上一次的更新

$\Delta w(t)=-\varepsilon \partial E / \partial w(t)+\alpha \Delta w(t-1)$

上面的偏导数在隐藏层和隐藏层的计算方式是不一样的；当前的神经元，误差会来自上面所有相连的神经元

观点

这种梯度计算的方式，通常会陷入到误差函数中局部最小值中；但是，经验表明陷入局部最小值，并不一定使得网络特别差；只有在connections足够多的情况下，这里应该是指全连接层太长了？
添加一点点连接层，会使得权重空间的维数增大（参数量多了），那么，绕开这种陷入局部最小值的路径就多了，所以比较好
总体来说，这样的学习过程，都是依据梯度来传递的；梯度传递的信息，是误差
这样的学习方式，真的是合理的吗？有没有一些生物学上的学习方式呢

问题

这篇文章介绍了反向传播，但是RNN的部分在哪呢？